
This is a big article.
Download it as a beautiful PDF to read later!
You will also get access to my popular Interesting Times newsletter where I share links to similar articles, tools and lots more.
One of the most frequent questions I get from readers is “How do I win at Russian Roulette?”
I’m sure you can relate. You’re standing in the dairy aisle at the grocery store and a stranger walks up to you and says “Hey! I have revolver in my car with one bullet in the chamber, wanna play Russian Roulette?”
And you’re like “Oh man, that sounds awesome. I’ll bring my friends and we can make it a game night.”
It makes sense. After all, 5 out every 6 Russian roulette players recommend it as a fun and profitable game.
No? You haven’t had a similar experience? That’s probably good. But, now that we’re on the topic, how do you consistently win at Russian Roulette? More to the point, what other scenarios like Russian Roulette exist where winning once is feasible but winning consistently is highly improbable?”
The rules for Russian roulette are simple: you sit in a circle with five other people, put one bullet in a pistol with six chambers, and each person takes a turn pointing the gun at their head and pulling the trigger.
You might roll the dice and take $1,000,000 to play Russian Roulette one time (though I wouldn’t advise it). But there’s no amount of money that would make you play it 6 or more times.
There are only two ways to consistently win Russian Roulette:
- DO NOT PLAY.
- Change the Rules1
Though you will (hopefully) never play Russian roulette, there are a surprising number of scenarios in life that have rules very similar to Russian Roulette but which otherwise sane and rational-seeming people (including Nobel prize winners) choose to play. In fact, you may be playing one of those games right now and don’t realize it.
How do you recognize games like Russian Roulette where the only way to win is to not play? And how can you change the rules to make it work more favorable for you?
The key is a big little idea called ergodicity.
What I Learned Losing 56 Million Dollars
Consider the following thought experiment offered by Black Swan author Nassim Taleb.
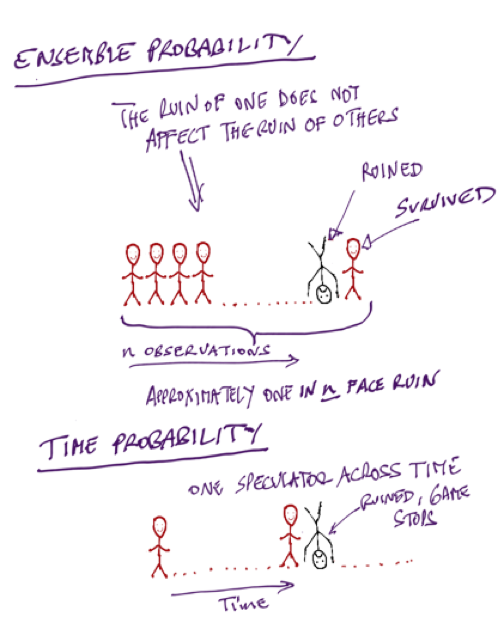
In scenario one, which we will call the ensemble scenario, one hundred different people go to Caesar’s Palace Casino to gamble. Each brings a $1,000 and has a few rounds of gin and tonic on the house (I’m more of a pina colada man myself, but to each their own). Some will lose, some will win, and we can infer at the end of the day what the “edge” is.
Let’s say in this example that our gamblers are all very smart (or cheating) and are using a particular strategy which, on average, makes a 50% return each day, $500 in this case. However, this strategy also has the risk that, on average, one gambler out of the 100 loses all their money and goes bust. In this case, let’s say gambler number 28 blows up. Will gambler number 29 be affected? Not in this example. The outcomes of each individual gambler are separate and don’t depend on how the other gamblers fare.
You can calculate that, on average, each gambler makes about $500 per day and about 1% of the gamblers will go bust. Using a standard cost-benefit analysis, you have a 99% chance of gains and an expected average return of 50%. Seems like a pretty sweet deal right?
Now compare this to scenario two, the time scenario. In this scenario, one person, your card-counting cousin Theodorus, goes to the Caesar’s Palace a hundred days in a row, starting with $1,000 on day one and employing the same strategy. He makes 50% on day 1 and so goes back on day 2 with $1,500. He makes 50% again and goes back on day 3 and makes 50% again, now sitting at $3,375. On Day 18, he has $1 million. On day 27, good ole cousin Theodorus has $56 million and is walking out of Caesar’s channeling his inner Lil’ Wayne.

But, when day 28 strikes, cousin Theodorus goes bust. Will there be a day 29? Nope, he’s broke and there is nothing left to gamble with.
The central insight?
The probabilities of success from the collection of people do not apply to one person. You can safely calculate that by using this strategy, Theodorus has a 100% probability of eventually going bust. Though a standard cost benefit analysis would suggest this is a good strategy, it is actually just like playing Russian roulette.
The first scenario is an example of ensemble probability and the second one is an example of time probability. The first is concerned with a collection of people and the other with a single person through time.
What is Ergodicity?
This thought experiment is an example of ergodicity. Any actor taking part in a system can be defined as either ergodic or non-ergodic.
In an ergodic scenario, the average outcome of the group is the same as the average outcome of the individual over time. An example of an ergodic systems would be the outcomes of a coin toss (heads/tails). If 100 people flip a coin once or 1 person flips a coin 100 times, you get the same outcome. (Though the consequences of those outcomes (e.g. win/lose money) are typically not ergodic)!
In a non-ergodic system, the individual, over time, does not get the average outcome of the group. This is what we saw in our gambling thought experiment.
A way to identify an ergodic situation is to ask do I get the same result if I:
- look at one individual’s trajectory across time2
- look at a bunch of individual’s trajectories at a single point in time
If yes: ergodic.
If not: non-ergodic.
We tend to think (and are taught to think) as though most systems are ergodic. However, pretty much every human system is non-ergodic. By treating things that are non-ergodic as if they are ergodic creates a risk of ruin, as cousin Theodorus found out. If you want to not die or go bankrupt, ergodicity is an important idea to understand.
This is particularly true in the case of financial education. Most finance material assumes ergodicity (that time and ensemble probabilities are the same) even though it is never the case.
If I lose all your money, you are in no way comforted that other people who you don’t know did fine. Even if their assessment of the probabilities were right, no person can get the returns of the market unless they have infinite pockets.
If the investor has to eventually reduce his or her exposure because of losses, or margin calls, or because of retirement, or because a loved one got sick and needed an expensive treatment, the investor’s returns will be divorced from those of the market.
This is why examples such as “If you had bought Amazon stock in 1999 and held it for 20 years, you would have done great even” are dumb. From 1999, the price of the stock collapsed by over 90%. The type of person that bought a bunch of Amazon stock in 1999 probably also bought a bunch of other crap stocks and had a job in tech. In 2001, they had to sell everything to make rent.
How (Not) to Lose All Your Savings
Consider the example of a retiring couple, Nick and Nancy, both 63 years old. Through sacrifice, wisdom, perseverance – and some luck – the couple has accumulated $3,000,000 in savings. Nancy has put together a plan for how much money they can take out of their savings each year and make the money last until they are both 95.
She expects to draw $180,000 per year with that amount increasing 3% each year to account for inflation. The blue line describes the evolution of Nick and Nancy’s wealth after accounting for investment growth at 8%, and their annual withdrawals and shows their total wealth peaks at around age 75 near $3.5 million before tapering off aggressively toward 95.
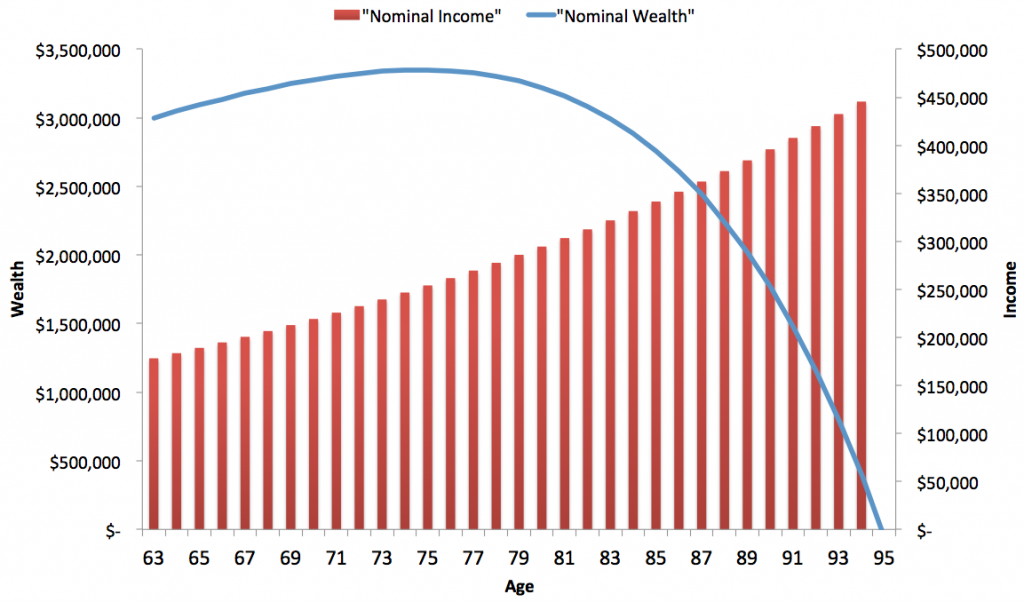
For the sake of this example, let’s assume that Nick and Nancy know for sure that their average annual return will be 8% over this 32 year period. That’s great, they’re guaranteed to have enough money then, right?
Turns out, no. It is non-ergodic and so it depends on the sequence of those returns. From 1966 to 1997, the average return of the Dow index was 8%. However those returns varied greatly. From 1966 through 1982 there are essentially no returns, as the index began the period at 1000 and ended the period at the same level. Then, from 1982 through 1997 the Dow grew at over 15% per year taking the index from 1000 to about 8000.
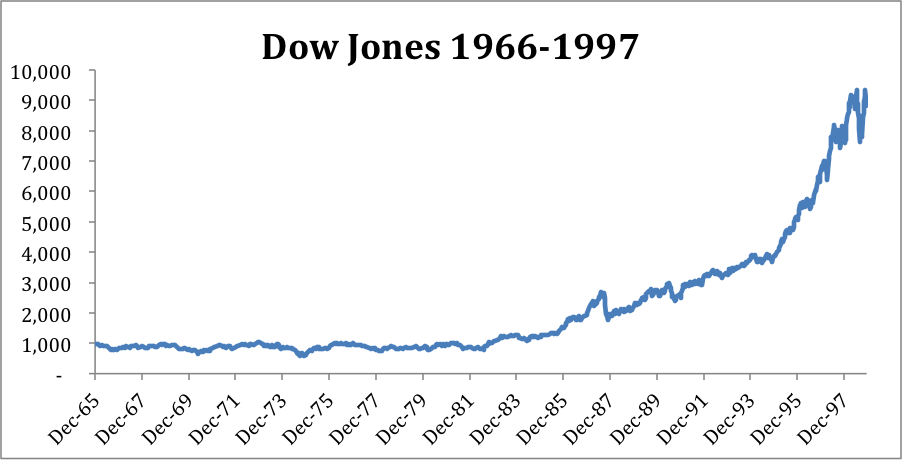
Even though the return average out at 8%, the implications for Nick and Nancy vary dramatically based on what order they come in. If these big positive returns happen early in their retirement (blue line), they are in great shape and will do much better than Nancy’s projections.
However, if they get the returns in the order they actually happened, with a long flat period for the first 15 years, they go broke at age 79 (green line).3
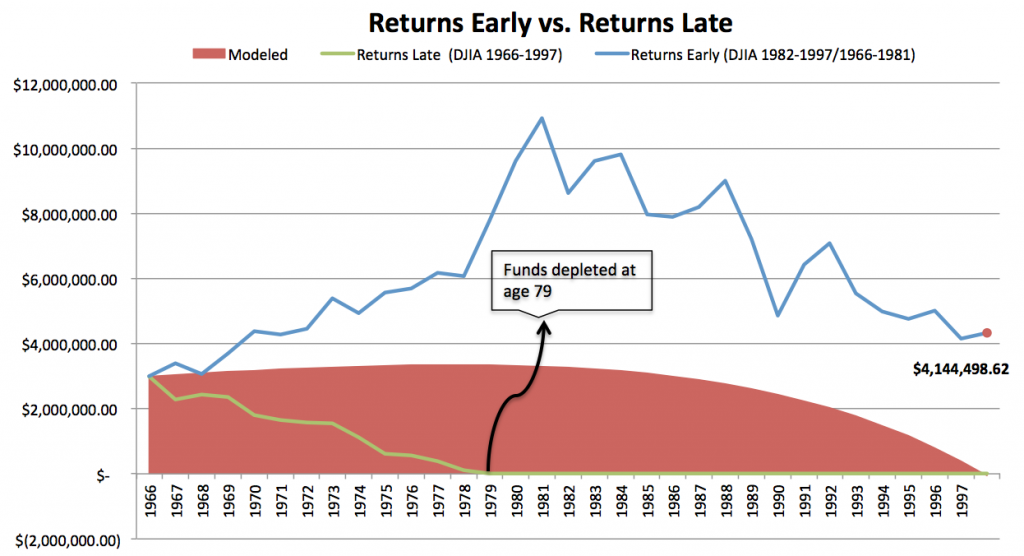
Sequencing matters. If big positive returns come early, Nick and Nancy are in great shape (blue line). If they come late (green line), they are ruined.
The model is assuming ergodicity, but the situation for Nick and Nancy is non-ergodic. They cannot get the returns of the market because they do not have infinite pockets. In non-ergodic contexts the concept of “expected returns” is effectively meaningless.
The Story of Long-Term Capital Management
Misunderstanding ergodicity is not just some mistake made by “dumb retail” investors like Nick and Nancy. Long-Term Capital Management (LTCM) was founded in 1994 by John W. Meriwether, the former vice-chairman and head of bond trading at Salomon Brothers. Members of LTCM’s board of directors included Myron S. Scholes and Robert C. Merton, who shared the 1997 Nobel Memorial Prize in Economic Sciences.
The story of LTCM reads just like Cousin Theodorus. LTCM was Initially successful with an annualized return of over 21% (after fees) in its first year, 43% in the second year and 41% in the third year. I can only assume Meriwether was walking around the office making it rain Lil Wayne style.
In 1998, it lost $4.6 billion in less than four months.4
In the long run, LTCM’s models were right. Their positions were eventually liquidated at a profit. However, they were not the ones that realized that profit. In the short run, they died, being forced to sell in a bailout orchestrated by Wall St. banks.5
LTCM’s collapse stemmed in part from their use of only five years of financial data to prepare their mathematical models, thus drastically under-estimating the risks of a profound economic crisis.

By definition, it is unlikely that a 1 in 20-year event would show up in five years of data, but substantially more likely it would show up within 20 years.
This same logic is pervasive in how most people think about their businesses. It’s entirely possible to correctly assess the probabilities that a new initiative is profitable and still go bankrupt. If you have a product which costs $1,000 to develop and a 1% chance of generating $1 million, it is positive expected value (1% * $1 million = $10,000). On average, this product generates a 10x return on investment. However, pursuing this strategy repeatedly guarantees that you will eventually file for bankruptcy.
Economics often evaluates people as playing ergodic games, while subjects are often making choices as if game is non-ergodic. As Gerd Gigerenzer has pointed out, “irrational” behaviors or “cognitive biases” are actually individuals realizing that a system is non-ergodic and not optimizing for expected value.
In Search of Antifragility
The central concept of Nassim Taleb’s Antifragile is the notion that there are two opposing ways in which something can respond to volatility: fragile things are harmed by volatility, while antifragile things benefit from it.
Fragility implies more to lose than to gain from volatility and more downside than upside. Antifragility implies more to gain than to lose, more upside than downside. You are antifragile to a source of volatility if potential gains exceed potential losses (and vice versa).
Fragile and antifragile can effectively be used as synonyms for non-ergodic and ergodic. A fragile actor is non-ergodic, a truly antifragile actor is ergodic.
If you want to determine whether something is fragile or antifragile, you expose it to volatility and see how it responds. Say you measure that when traffic increases by a thousand cars in a city, travel time grows by ten minutes. But if traffic increases by another thousand more cars, travel time now extends by an extra thirty minutes. Such acceleration of traffic time shows that traffic is fragile, the more volatile things get, the worse it gets.
If you graph a fragile system, there is limited upside and unlimited downside. If the traffic is very light, you might get to your destination five minutes faster. If it is very bad, it may take an hour. There is a negative asymmetry.
If you graph an antifragile system, there is limited downside and unlimited upside. Going to cocktail parties is antifragile – you can only lose a bit of time (limited downside) but you could meet someone who will change your life (unlimited upside).
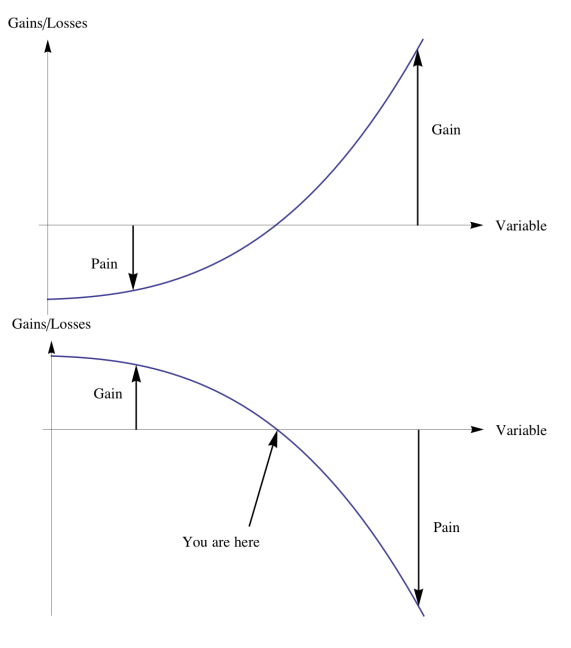
If you are fragile or non-ergodic, meaning there is some chance of blowing up, then it is guaranteed you will eventually blow up.
It’s important to note that if we stretched time to infinity, everything is nonergodic because all life will perish in the heat death of the universe, but this is not very helpful. We could say crossing the street is technically non-ergodic or fragile. However, in a single lifetime, it is effectively ergodic. The individual that crosses the street 1000 times gets the same returns as the ensemble. The question that is practically relevant is what time frame matters to you.
So what are the strategies that you can use to make your exposure more ergodic?
Going Ergodic
The approach to making yourself more ergodic in different scenarios is through diversification. Effective diversification can make non-ergodic situations more ergodic. There are two ways of thinking about diversification that I find helpful.
- The Barbell
- The Kelly Criterion
The Barbell
The Barbell is an approach that advocates playing it safe in some areas and taking a lot of small risks in others. That is extreme risk aversion on one side and extreme risk loving on the other, rather than just the “medium” risk attitude that is actually a version of Russian roulette.
One example applied to your career would be to get skilled in an extremely safe and predictable profession, say accounting or dentistry, while moonlighting in something extremely risk, say acting. Acting is extremely non-ergodic while accounting is much more ergodic. The two in combination are more ergodic than either alone.
Antifragility is a function of combining a multitude of entities so that each one of them is non-ergodic but the ensemble is ergodic. So you can make yourself more ergodic and antifragile by dividing yourself into an ensemble of entities able to fail independently without “carrying down” the others.
One common example of a barbell-like approach in investing is combining a portfolio of treasury bonds (supposedly very safe) with stocks (supposedly very risk). And indeed, over the last 30 years or so, stocks and treasury bonds have been mostly anti-correlated or uncorrelated
Similar to LTCM, this strategy’s challenges are exacerbated because it relies on data going back only thirty years. Looking back over the last 120 years of financial history, stock and bonds are more frequently correlated than anti-correlated.
If the relevant timeline here is one lifetime, the barbell strategy would suggest putting 80% of your portfolio into something less risky like maybe cash or unlevered real estate and 20% into something much riskier like angel investments or starting your own business.
What matters is not average correlation, but correlation during a crisis or black swan event. Take, for example, the size of safety exits in a theater. What matters is not whether they are large enough to pass through on average, but how easy they are to pass through during a fire.
The key from a financial perspective is to prepare for a situation where the markets drop and your job income gets hit at the same time. In one lifetime, it will likely happen. Volatility tends to cluster.
Or, as Vladimir Lenin put it “There are decades in which nothing happens and weeks in which decades happen.” Saying something is ergodic during the decades in which nothing happens is meaningless. The question is whether it is ergodic in the weeks in which decades happen.
One common piece of personal finance advice is to set up an emergency fund – keeping 3-12 months of your expenses in cash that you only touch in times of emergency. This is effectively a rule of thumb which increases ergodicity.
In a business context, this would look like diversifying different choke points in your business. If you rely on a single factory to do all your manufacturing, can you get another factory to do 20% of the work even if you pay more per unit just so you have a back up?
I often advocate an 70/20/10 marketing approach where you focus 70% of marketing spend on the most predictable, boring channel then get progressively more experimental with the 20% and 10%. If the experimental stuff fails, you’re still in good shape, but you have upside exposure if it works.
If you want to go nuts, you keep adding additional streams of diversified income, each stream may get destroyed at some point, but the whole will not.
The Kelly Criterion: Cap Bet Size
The Kelly Criterion is a betting strategy popularized by J. L. Kelly and Ed Thorpe based on Claude Shannon’s Information Theory. The key insight of the Kelly Criterion is that you never bet everything and you increase your risk as you are winning but decrease it when you are losing.
So if he were using the Kelly Criterion, cousin Theodorus would not bet using his entire winnings each day. He would take additional chips off the table as he started losing and put more back on if he was winning.
The Kelly Criterion optimizes for typical wealth not expected wealth. Said another way, it assumes markets are non-ergodic. In effect, this means that the Kelly criterion makes it impossible to go bankrupt which seems like a good idea.
The simplest version of the Kelly Criterion is:
Edge/Odds = Fraction of Bankroll to Allocate
The edge is the total expected value like we looked at initially, but it also incorporates the odds., To take a simple example, let’s say you’re offered a coin toss where heads you get $2 and tails you only lose $1.
Your odds are 2:1 (Bet $1 with the possibility of winning $2)
I built a super simple version of a Kelly Criterion calculator in Google Sheets if you want to make a copy and play around with it to get a feel for how it works.
Your expected value is $0.50 and your odds are 2, so you should bet 25% of your bankroll ($0.50/2)
The Kelly criterion is about bringing as much ergodicity as possible into non-ergodic realms.
Some way that this plays out in the real world would be to differentiate between “ergodic expenses” – expenses you can scale down if your income decreases and “non-ergodic expenses” – expenses you cannot scale down if your income decreases, such as debt (renegotiations withstanding). To increase the ergodicity, you would try to make both your liabilities and expenses as easy to scale down as possible.
Similarly, a founder of a company that sells a portion of the company to another investor like a private equity firm is using the Kelly Criterion. We even call it “taking chips off the table.
Conclusion
We are still in the very early days of understanding ergodicity and all the ways it applies to our lives.
If you have any thoughts, I’m on Twitter @TaylorPearsonMe.
Acknowledgments: Special thanks to Luca Dellanna who provided detailed feedback on an early draft of this article and has written a book on the subject. Additional thanks to Max Arb, Joe Norman, Ole Peters, and Rory Sutherland for Twitter discussions which illuminated many of these ideas.
Last Updated on June 11, 2025 by Taylor Pearson
Footnotes
- Malcolm X knew how to consistently win at Russian Roulette. During Malcolm X’s burglary career, he once played Russian roulette, pulling the trigger three times in a row while pointing it to his head to convince his partners in crime that he was not afraid to die. Malcolm X later revealed to a reporter that he palmed the round. Smart man.
- If we looked at one individual trajectory across an arbitrarily finite segment of time, it is possible to get the incorrect belief idea that the system is ergodic. For example, if we compared one individual playing two round of Russian roulette to two different individuals playing one around, it’s possible that the bullet would not go off in either case leading us to believe the system is ergodic even though it isn’t. This goes into epistemology and the problem of induction, both far outside the scope of the post but worth keeping in mind that the longer the timeline runs, the better.
- This example from PATH DEPENDENCY IN FINANCIAL PLANNING: RETIREMENT EDITION from Resolve Asset Management.
An example of one of the trade which costs LTCM was an arbitrage between Royal Dutch and Shell. LTCM had established an arbitrage position in the dual-listed company Royal Dutch Shell in the summer of 1997 when Royal Dutch traded at an 8%–10% premium relative to Shell. A dual-listed company is a corporate structure in which two corporations function as a single operating business through a legal equalization agreement, but retain separate legal identities and stock exchange listings.
This meant it didn’t make sense for Royal Dutch stock to be trading at a premium to Shell stock, they represented equal rights to future cash flows of the company.
By going long Shell and short Royal Dutch, LTCM was essentially betting that the share prices of Royal Dutch and Shell would converge because a basic evaluation would show that the present value of the future cash flows of the two securities should be similar.
- The premium of Royal Dutch increased from 8% to 22%. Because their models were being used in other, similar trades that also went bad in the short term, they had to unwind the position in Royal Dutch Shell at a loss of more than $140 million.

