Today, I’d like to tell you a little story about a farmer named Bill. If you’re not into farming, it just so happens that Bill discovers one of the most important principles in investing and decision-making in this story, so there’s also that.
Anyway, back to Bill. Bill grows crops. In a good season, Bill harvests 150 seeds for every 100 seeds that he plants. That’s a 50% growth rate!
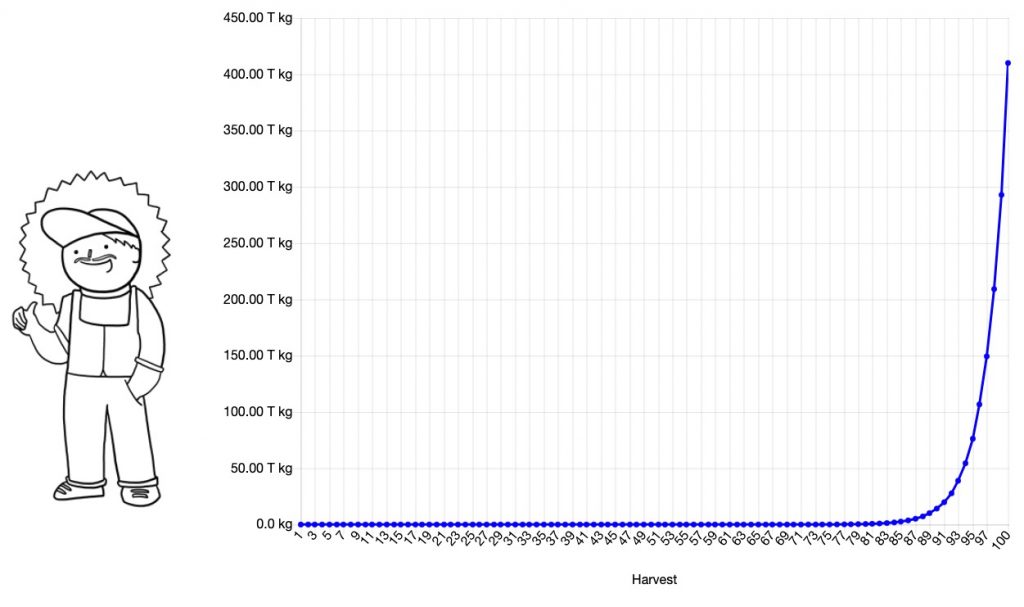
If Bill does that every year, his farming business will grow exponentially. 1 kilogram of seeds grows into 1.5kg of seeds in the first year. 1.5kg of seeds grows into 2.25kg of seeds the next year, then into 3.375kg of seeds the next year, and so on.
People are really bad at intuiting exponential growth (AKA compounding).
By year 100, his 1kg of seeds has grown to an astronomical 400 T kg.
However, farming is not so easy a business. Some times, Bill has bad harvests. In bad years, he only gets 70% of his seeds back, a loss of 30%. For Bill, good and bad seasons are equally likely and unpredictable. On average, half the years will be good and half will be bad. But, it’s possible to get “lucky” and have a streak of good years or “unlucky” and have a streak of bad years.
That’s not ideal as a smooth exponential growth curve, but it still seems pretty good, right? It’s a positive expected value bet: half the time you make 50% and the other half the time, you lose 30%. On “average,” you make 10%.
Let’s run the simulation over a hundred years this time and see how Bill does.
The first time I ran the simulation, Bill did pretty well. Things were choppy and he hadn’t made any progress for the first 20 years but then he had a run of good luck and ended up with over 1000kg of seeds. Not bad!
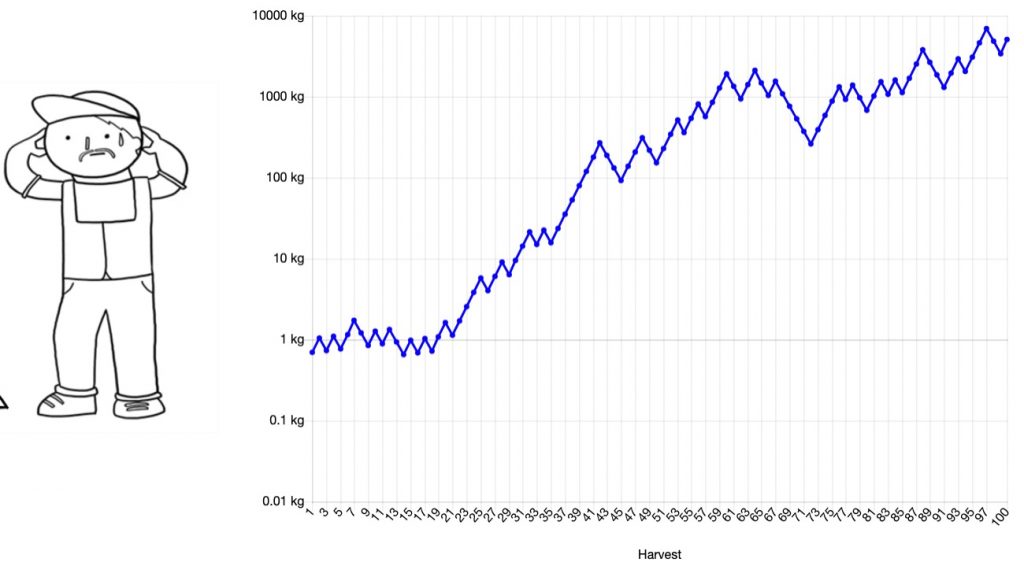
The second time I ran the simulation, Bill started with a run of bad luck. He had some tough years, losing almost 90% of his seeds before finally bouncing back and ending with a bit over 100kgs in seeds.
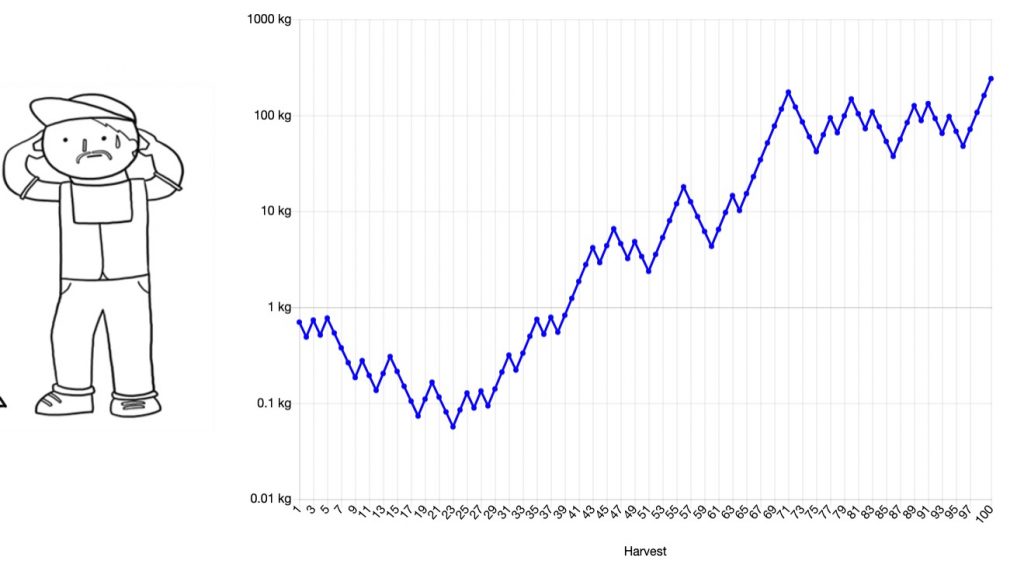
The next time I ran the simulation, Bill had a slow start followed by a lucky steak from years 17 to 45 then went sideways before ending on a tough run of luck with just over 10kg of seeds.
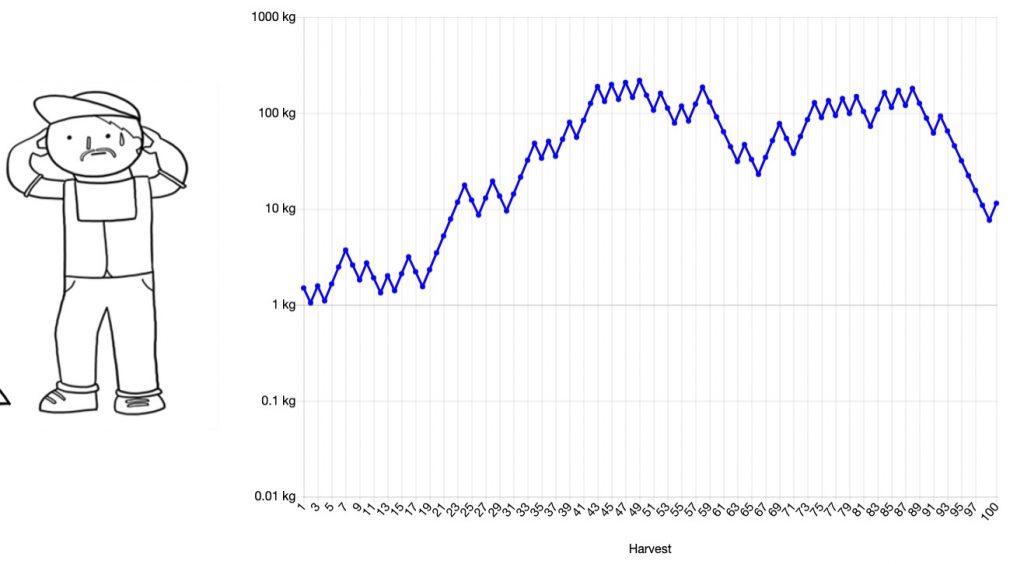
The fourth and final time I ran the simulation, Bill got off to a pretty good start but his luck turned around year 25 and he finished the 100 year period with less than he started with. That sucks!
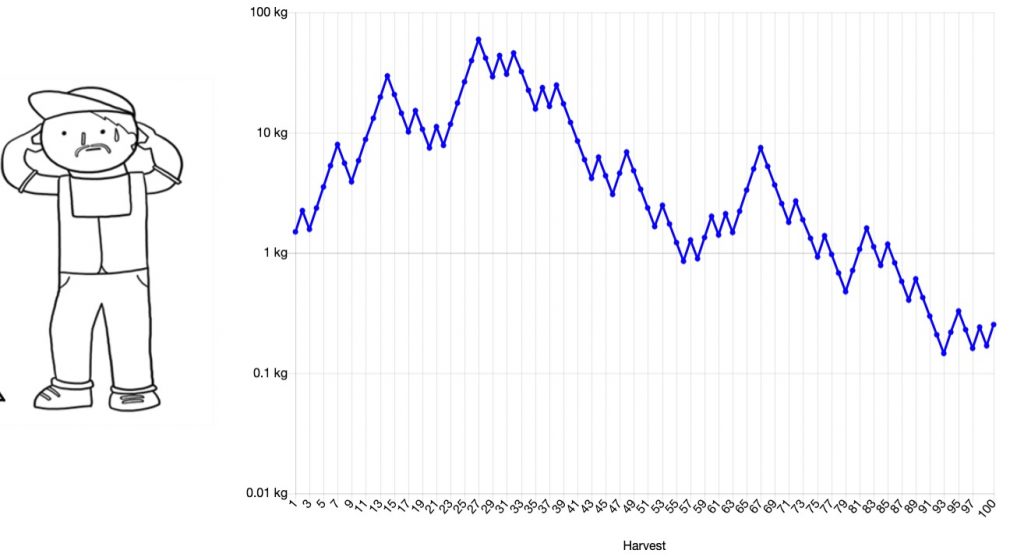
The thing that jumps out after running these simulations is that there is a lot of luck involved and the possible variety of outcomes is very wide. In just four simulations, Bill ended up anywhere between up 1000x where he’s watching over his farmland from his ski chalet to down 80% where he’s barely able to survive.
So while, “on average,” farming is a good business, Bill doesn’t get “average” returns over the course of his long farming career. He could do exceptionally well or exceptionally bad, depending on how the chips fall. (Said another way, farming is non-ergodic.)
That doesn’t seem like a very good business, there’s too much luck involved. Even though it works out “on average,” would you want to start a business or make an investment for your whole life time with that much variability? Probably not, it’s not similar to playing Russian Roulette for a million bucks – even though you win “on average,” there’s too much risk of getting “unlucky.”
What can Bill do?
Well, there’s another farmer named Ann. Ann’s crop yield follow the same rules as Bill’s yields: half the time she makes 50%, and half the time she loses 30%, for an average return of 10%.
However, Bill and Ann live on opposite ends of the country and so the weather patterns affecting their crops are unrelated. Bill having a bad year doesn’t make it any more or less likely for Ann to have a bad year and vice versa. They are independent variables and it’s random as to whether each one will have a good or bad year.
Let’s run a simulation with both Bill and Ann. In this simulation, Bill ends up relatively lucky, ending with 1611kg, and Ann is relatively unlucky, ending up with just 16.6kg.
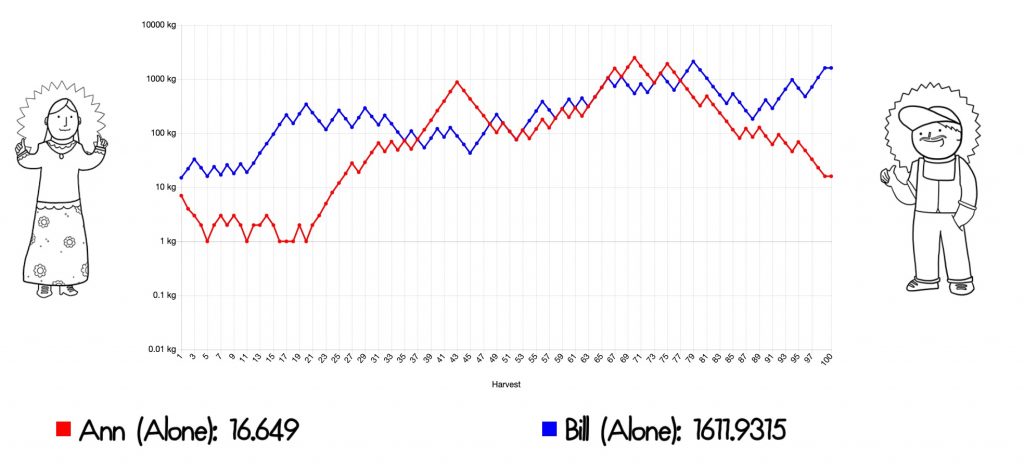
But what if they make a deal? At the end of every season, Ann and Bill agree to share their harvests equally.
In investing terms, they are agreeing to “rebalance” their profits and losses. If Ann does well and Bill does poorly, she’ll share with him and vice versa.
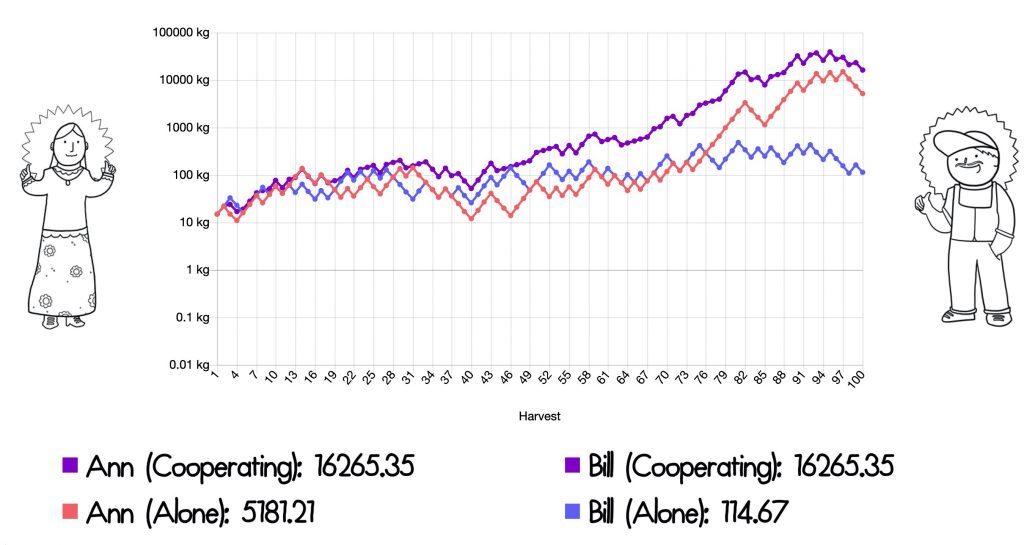
By cooperating, they both do much better. Each ends up with 16,265kg of seeds. Even though Bill was lucky and did much better than Ann, he did 10x better by cooperating and sharing with Ann then by going it alone.
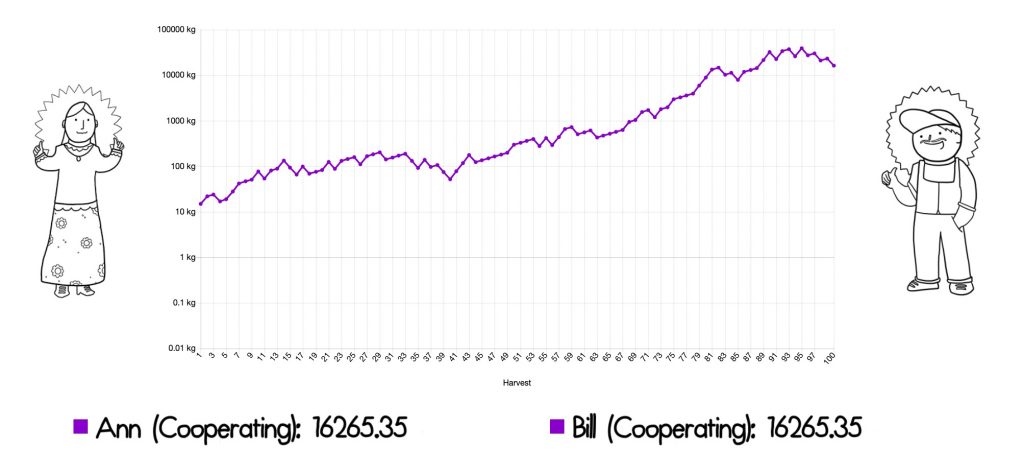
Was this just a lucky simulation?
In a sense, there is luck involved because the good and bad years are random.
But, over the long run, luck becomes a certainty.
When you have two positive expected value bets or outcomes that are uncorrelated (Ann having a good year doesn’t make it more or less likely for Bill to have a good year – that means they are uncorrelated) or even anti-correlated, then rebalancing them increases the long-term returns and decreases risk.
In Ann and Bill’s case, pooling and sharing both reduces risk and increases growth for everybody involved.
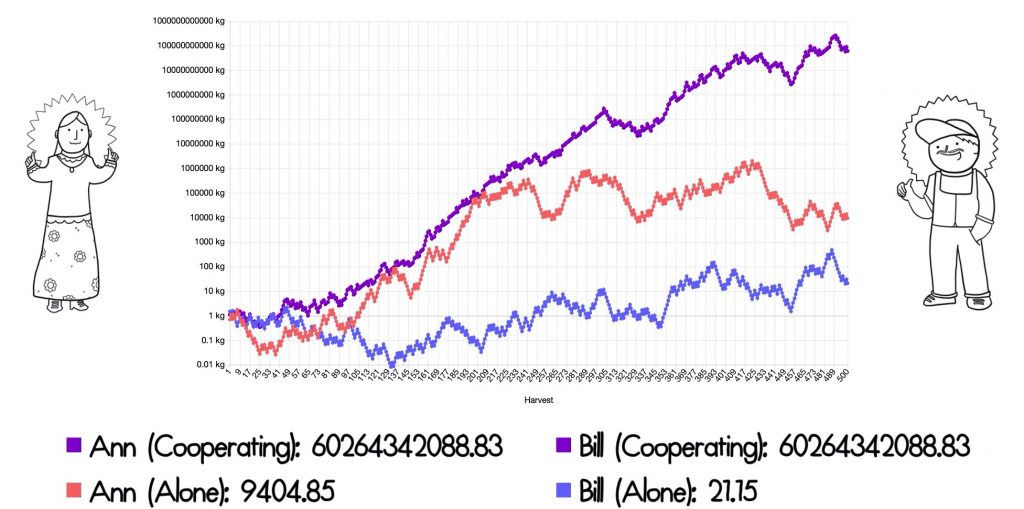
It’s pretty crazy just how much it improves growth and reduces risk. In this 500 year simulation, Bill would have finished with just 21kg but by cooperating, he finished with over 60 billion kg – 60,265,342,088kg. That’s a big difference!
Anything that grows exponentially, or compounds, grows faster when you rebalance or share resources.
This is pretty counterintuitive, how can Ann and Bill together do so much better than Ann and Bill alone? Let’s walk through an example.
Both Ann and Bill start out with 1 bundle of wheat. Ann has a very good first year and triples her harvest. The next year, she just manages to break even and finishes with three bundles.
Bill starts out with a tough first year and just manages to break even, ending with one bundle of wheat. In the second year, Bill does really well and triples his wheat, also ending with three bundles.
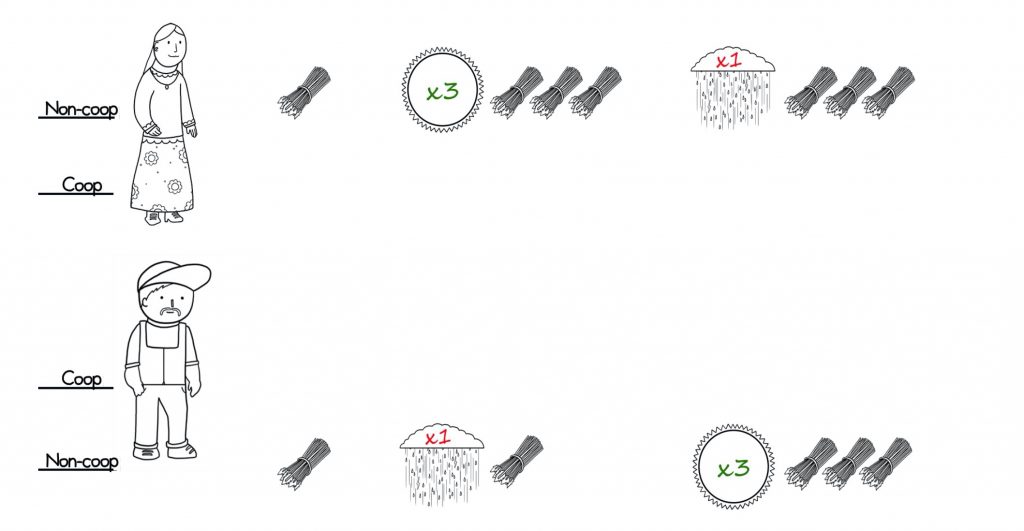
Now, imagine they shared or rebalanced their wheat after each year.
Ann has a good first year again and Bill has a tough first year, just like the first time around.
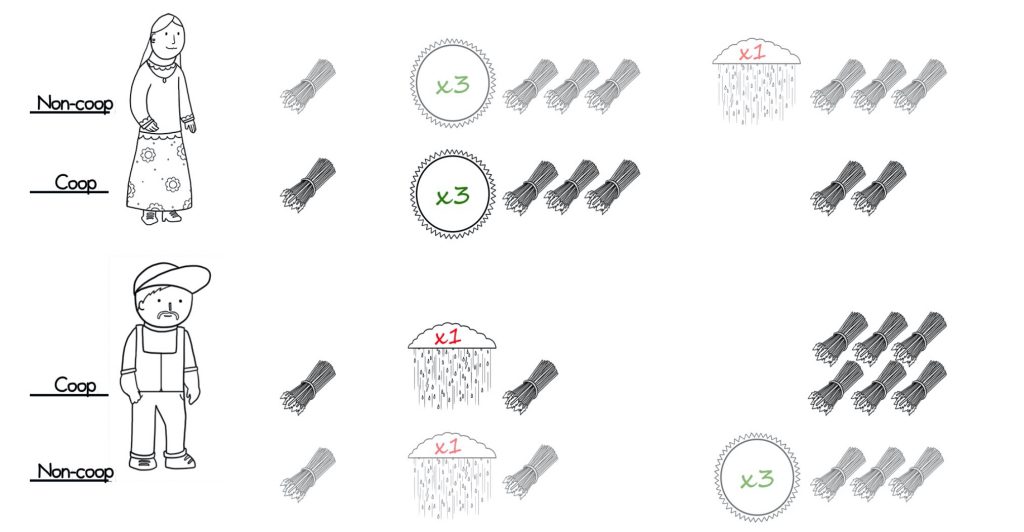
This time, Ann shares some of her profits with Bill so they both end up starting their second year of farming with two bundles of wheat.
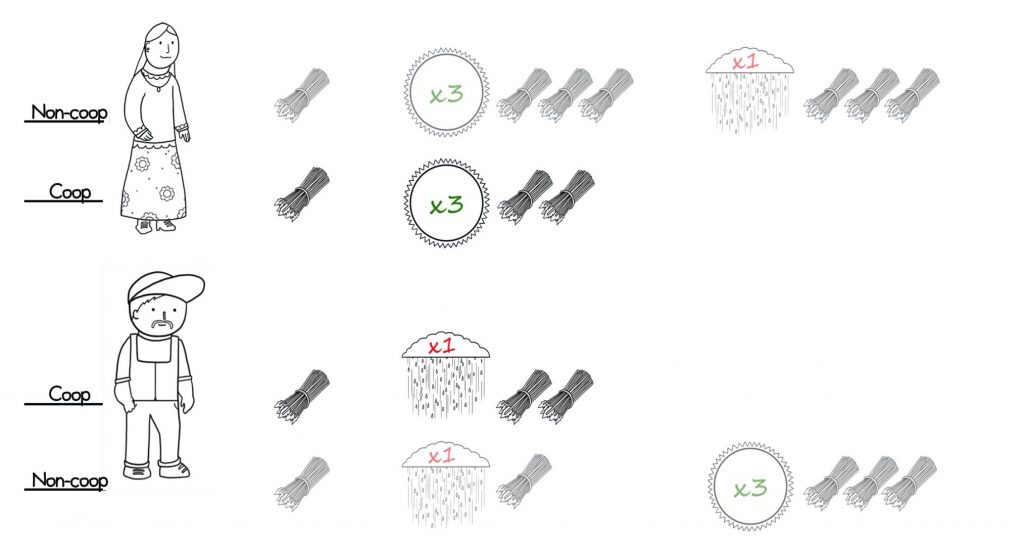
In the second year, Bill has a good year and manages to triple his two bundles into six bundles. Ann has a tough year and ends up with just the two bundles that she started with.
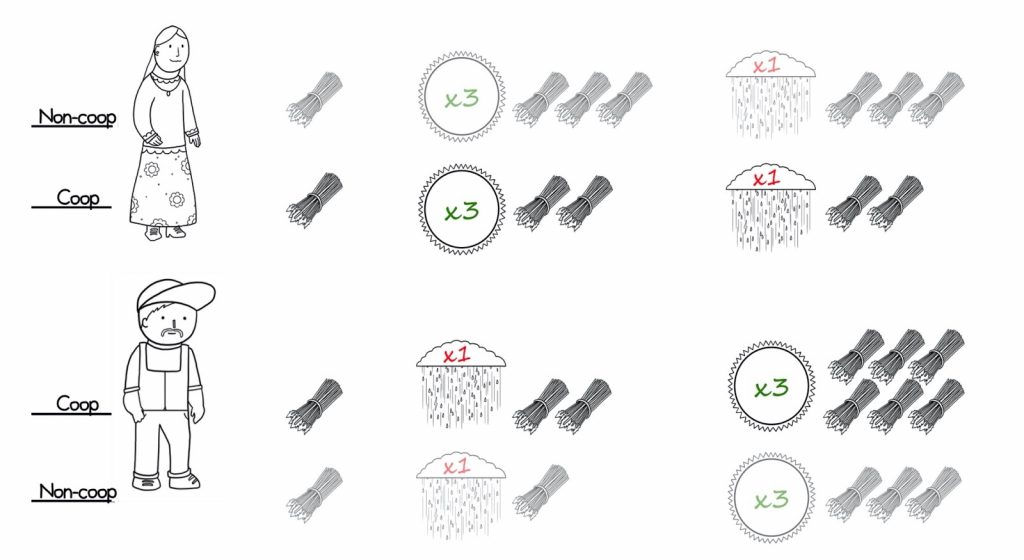
But, they’ve agreed to share and so Bill gives Ann two of his bundles. They both finish the second year with four bundles.
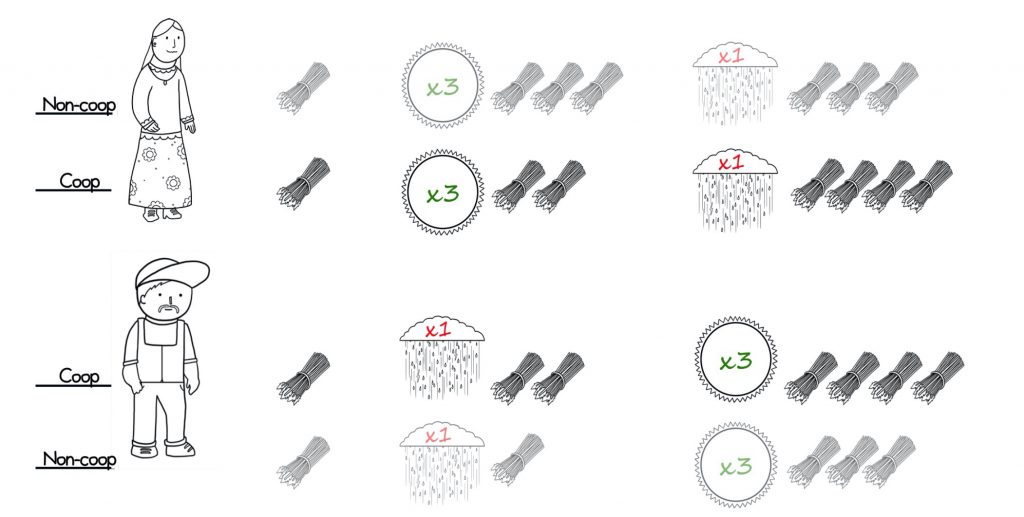
By the magic of diversification and rebalancing or sharing, we’ve created two bundles of wheat without changing the odds of the game at all!
Investors say that “diversification is the only free lunch in investing” and this is how that free lunch happens.
By combining a portfolio of positive expected return1 but uncorrelated or anti-correlated bets, you get a better performing portfolio. Most people don’t think about their investment portfolio this way.
To make better risk-adjusted returns, it’s really hard and competitive to try and be a better picker of assets. It’s comparatively much easier to build a portfolio of diversified bets and harvest the rebalancing premium between them.
Most investors look at each individual piece on its own: “which of these companies is going to do the best and I should put all my money in that one?”
The correct way to think about it is “I should put some of my money in the investment that I think is going to do the best and then also put some in investments that I think won’t do as well but are uncorrelated or anti-correlated because if I rebalance between them, I improve the overall performance of the portfolio.”
Investors tend to be overly focused on the best investment when what really matters is the best portfolio. In our simulation where Bill did much better than Ann, he still did even better by sharing or rebalancing with her. The investor that put 100% of their investment into Bill’s farm and successfully “picked the winner” did worse than the investor that put half in Ann’s farm and half in Bill’s farm and rebalanced each year.
While this lesson has obvious implications for investors, it applies in many areas of our lives. Self-help cliches like “your network is your net worth” suddenly make a bit more sense. If you have a lot of people willing to share with you and collaborate, it quite literally increases your long term net worth. Helping out a friend, neighbor, or someone on the other side of the world that’s had a tough run of luck is a form of societal “rebalancing.”
At some point in the future, you’ll be the one with the string of bad luck and having a network that’s willing to help out will be better for you and better for them.
Though this lesson seems a bit counterintuitive, there’s an interesting and compelling argument that it’s hardwired into our biology. Humans, chimps, and many other animals have an extremely pronounced tendency to engage in reciprocity. The lion that shares the zebra she killed with the rest of the pride is not just being nice, she is improving her chances of surviving and reproducing because she knows that the other lions will do the same at some point in the future.
It makes sense that animals who behave this way would thrive over those who don’t. Bill and Ann’s farming business will do much better in the long run than some farmer going at it alone.
All images and this story credit to FarmersFable.org which has a wonderful interactive game that demonstrates this principle.
Last Updated on July 27, 2020 by Taylor Pearson

